Ứng Dụng “Toán Học Bình Dân” trong một Phương trình 2 Ẩn Số

Qua nhiều lần trao đổi thư tín giữa bạn bè & độc giả, một số vấn đề được nêu ra.

Vấn đề thứ nhất TS Lưu Nguyễn Đạt đưa ra:

[1] định nghia, xác định, chứng minh “Toán Học Bình Dân”
[2] ứng dụng “Toán Học Bình Dân” trong quá khứ [địa điểm/địa hạt] ra sao?
[3] ứng dụng “Toán Học Bình Dân” trong hiện tại/tương lai [địa điểm/địa hạt] như thế nào?

 Hoàn toàn đúng, xác thực, đôi khi 3 vấn đề đó là điều kiện cần phải có “ắt có và đủ” để được gọi là “TOÁN HỌC BÌNH DÂN”. Thưa TS  tôi có chứng minh, nhưng chứng minh rất đơn giản, còn Toán Học Bình Dân là vấn đề lớn cuả DÂN TỘC, không thể do một mình tôi tự quyết định mọi vấn đề, mục đích tôi dưa ra một số ứng dụng thực tế, để quý độc giả trong ngoài thấy có lý, khả thi, thì quý GS, TS quý Độc giả có quan tâm đến Toán học, chúng ta ngồi lại với nhau vạch ra chương trình cuả Toán Học Bình Dân trong đó có định nghĩa, định lý đầy đủ…
Để tỏ lòng trân trọng độc giả, dù độc giả là Học sinh Sinh viên trong cũng như ngoài nước, tôi có trình bày sơ qua một đoạn trong bài viết trước đây cũng trên khoahoc.net, muốn được Cộng đồng Toán học công nhận, phải có chứng minh, phải được trình qua Hội Đồng Toán Học, thời gian chờ đợi được công nhận hay không ít nhất là 2 năm, lúc đó mới có quyền nói.

Những bài toán bình dân

CHỢ TẾT

Một quan tiền(*) tốt mang đi,
Nàng mua những gì mà tính chẳng ra?
Thoạt tiên mua ba tiền gà, (180)
Tiền rưỡi gạo nếp với ba đồng trầụ (93)
Trở lại mua sáu đồng cau, (6)
Tiền rưỡi miếng thịt, giá rau mười đồng. (100)
Có gì mà tính chẳng thông.
Tiền rưỡi gạo tẻ, sáu đồng trà tươị (96)
Ba mươi đồng rượu, chàng ơi, (30)
Ba mươi đồng mật, hai mươi đồng “vàng”.(50)
Hai chén nước mắm rõ ràng,
Hai bảy mười bốn kẻo chàng hồ nghị (14)
Hăm mốt đồng bột nấu chè, (21)
Mười đồng nải chuối, chẵn thì Một Quan! (10)
(Phong Dao)
——————————————————

 cộng lại                                                                  600

(*)Cụ Hoàng Ngọc Liên cho biết 1 quan = 600 đồng

                                                                   1 tiền = 60 đồng

 

PHÚ ÔNG
 
Phú ông cỡi ngựa thăm đồng
Thấy thằng chăn vịt, Phú ông hỏi liền
Vịt bầy, mầy có mấy con
Nói ngay, sao đúng, tao còn tha cho.
 
Anh chàng chăn vịt trả lời
Bầy nầy, bầy nữa ông ơi
Nửa bầy nữa, một phần tư bầy nữa
Cộng con ngựa, đủ trăm con
Khó gì, mà tính không ra
Phú ông trố mắt đứng nhìn
Ai người giỏi toán, Phú ông xin nhờ
 

Cách giải

Goi x là số vịt

Theo đề ta có:                x + x + x/2 + x/4 = 99          (100 trừ con ngựa)

Hóa đồng mẫu số cộng lại

                                                        11x/4  = 99

Suy ra                                                     x  = 36

 đáp số 36 con

———————

100 TRÂU ĂN 100 BÓ CỎ
Trâu đứng ăn 5
Trâu nằm ăn 3
5 trâu con ăn 1
Hỏi mỗi thứ mấy con
 

Bài toán 100 trâu ăn 100 bó cỏ

Cách giải 1

Gọi trâu đứng = x, trâu nằm = y, trâu con = z 

viết phương trình:

                     x  +   y +  z       =  100

                   5x + 3y + 1/5 z   =  100

Nhân phương trình dưới với 5 để loại bớt z :

                    25x + 15y + z    =   500

                    -( x  +   y +  z     =  100)

————————————————–

                    24x  +  14y        =   400

hay 

                        12x  +  7y      =   200     (1)

Phương trình (1) chứa 2 ẩn số x và y. Thông thường mỗi ẩn số phải có một phương trình ta mới giải được, ở đây 2 ẩn số trong một phương trình, Phương Tây gọi phương trình nầy là Diophantine Equation

Từ năm 2100 đến năm 1600 trước Công nguyên người Babylon, đã giải thành thạo các phương trình có dạng:

                     2x² – y²  = 1

Như vậy phương trình bậc 1 của Tiền nhân ta phải có trước  phương trình bậc 2 của người Babylon

Ta có thể nói bài toán “trăm trâu ăn trăm cỏ” là bài toán Nguyên thuỷ của Diophantine Equation,

Theo đề trâu đứng ăn 5 bó, giả sử trâu đứng ăn 100 bó cỏ thì tối đa là 20 con,  x phải nhỏ hoặc bằng 20 (x ≤ 20).

Thay lần lượt các trị số của x để tìm y (y phải nguyên):

                            y   =   (200 – 12x)/7

Ta có

Đáp số 1:

trâu đứng       x = 5 con
trâu nằm        y = 20 con
trâu con         z = 75 con

Đáp số 2: 

trâu đứng      x = 12 con
trâu nằm       y =   8 con
trâu con        z =  80 con

Cách giải 2

Giải như trên thấy không ổn, nên tôi có cách giải khác hơn nhưng vẫn có cùng kết qủa như trên

Gọi
trâu đứng = TĐ
trâu nằm  = TN
trâu con   = TC 

                             GIẢI

Nhóm 1:
                        1TĐ ăn 5 bó cỏ
                        5TC ăn 1  –   –

1TĐ + 5TC  tương đương  6 bó cỏ  (1)

Nhóm 2: 
                        4TN ăn 12 bó cỏ

                        10TC ăn 2   –   –
 4TN + 10TC  tương đương 14 bó cỏ (2)
Từ (1) và (2) chúng ta viết phương trình tương đương:

 0mod(1TĐ +5TC) + 0mod(4TN+10TC) ≡  100 Trâu
                  và   0 mod 6    +  0 mod14     ≡  100 bó cỏ

Giải phương trình tương đương nầy chúng ta có hai đáp số sau đây:

Đáp số 1:

  trâu đứng (TĐ) =  5 con
  trâu nằm  (TN) = 20 con
  trâu con   (TC) = 75 con

 Đáp số 2: 

  trâu đứng (TĐ) = 12 con
  trâu nằm  (TN) =  8 con
  trâu con   (TC) = 80 con

Những bài toán xuất phát từ nông dân, nên tôi tạm gọi “TOÁN HỌC BÌNH DÂN” chứ chưa gọi chính thức.

Mong Quý Vị thông cảm cho, cũng như các nhà Toán học đã từng thông cảm cho tôi khi trình Luận án lớn (Fermat’s Last Theorem) mà không có trường Đại học hay một GS nào đở đầu, nhưng vẫn được Cộng đồng toán học đón nhận

Vấn đề thứ 2 TS Lưu Nguyễn Đạt đã nêu ra

“Trong phần “Chứng minh Định lý Lớn”, tôi thấy GS có nhắc tới phương pháp quy nạp [inductive method], tôi nghĩ phần đối ứng sẽ liên hệ tới phương pháp suy diễn [deductive method] trong hệ thốngToán học Bình dân.  Mong GS có dịp chỉ dẫn thêm trong tương lai.  Thân, LNDat”

Dạ không dám chỉ dẫn đâu ạ, nhưng xin phép Dr cho tôi được trình bày hơi dài dòng một tí, không ngoài mục đích, để các bạn trẻ tự hào về Tiền nhân cuả chúng ta.

Phương pháp quy nạp tối cần thiết cho các phương trình có số mủ lớn, thật lớn, có khi số mủ tiến đến vô cự, trường hợp cụ thể như Định lý sau cùng cuả Fermat “xⁿ + yⁿ = zⁿ 

n > 2 phương trình vô nghiệm”, vì n = 2 có vô số nghiệm, nên các nhà Toán học không thể áp dụng phương pháp quy nạp để chứng minh những n ≥ 3 là vô nghiệm, bằng chứng

qua internet chúng ta thấy các nhà toán học từ thế kỷ XVIII đến nay làm việc rất khó khen, khi chứng minh số  mủ n ở một thời điển nào đó là vô nghiệm, xin đơn cử sơ qua như

 

Euler wrote to Goldbach on 4 August 1753 claiming he had a proof of Fermat’s Theorem when n = 3

 n = 4 case of  Piere de Fermat

 1825. In fact Dirichlet was able to complete his own proof of the n = 5

 In 1832 Dirichlet n = 7 và n = 14

 The n = 7 case was finally solved by Lamé in 1839

 1983 – the classification of finite simple groups, a collaborative work involving some hundred mathematicians and spanning thirty years, is completed,

1987 – Yasumasa Kanada, David Bailey, Jonathan Borwein, and Peter Borwein use iterative modular equation approximations to elliptic integrals and a NEC SX-2 supercomputer to compute π to 134 million decimal places,

 Using techniques based on Kummer‘s work, Fermat’s Last Theorem was proved true, with the help of computers, for n up to 4,000,000 by 1993

 

Nếu chỉ xem timeline trên đây chúng ta không đủ can đảm nghỉ, hay nói tới Fermat’s Last Theorem, chứ đừng nói là tìm cách chứng minh định lý, Euler nhà toán học nổi tiếng cuả thế kỷ, cũng chỉ chứng minh được n = 3 là vô nghiệm, hoặc hàng trăm nhà Toán học cộng tác với nhau, làm việc trong 30 năm liền, hay các nhà toán học Yasumasa Kanada, David Bailey, Jonathan Borwein, and Peter Borwein cùng với computer hiện đại nhất củng chỉ chứng minh được một phần rất nhỏ, mới đi đoạn đường ngắn thôi

Trong lúc chúng ta không có gì trong tay, chẳng lẻ chúng ta cứ ngồi chờ các nhà Toán học, phát minh cái nầy cái nọ, để chúng ta học ngày học đêm, rồi tự hào, thì biết bao giờ ta mới bắt kịp họ, chứ đừng nói là hơn họ.

Tôi đồng ý với TS Lưu Nguyễn Đạt đã nói: phương pháp suy diễn [deductive method] là phương pháp tốt nhất để chúng ta hình thành môn học cỗ xưa đó chính là “TOÁN HỌC BÌNH DÂN”.

Sơ dĩ tôi nói cổ xưa vì mới đây các nhà Khảo cổ đã tìm thấy khúc xương hóa đá có niên đại từ bốn chục ngàn, đến ba chục ngàn năm trước Công nguyên (40.000 – 30.000) trong vùng núi Phi châu, đặt biệt trên khúc xương hóa đá nầy, các nhà khảo cổ đã tìm thấy những ghi chép của người xưa. Họ đã biết dùng các số để ghi nhớ con vật đã săn bắt được, những dấu vết khắc trên xương làm điên đầu các nhà Khảo cổ, nhưng rồi họ cũng đồng ý với nhau bằng những con số, như sơ đồ minh hoa dưới đây:

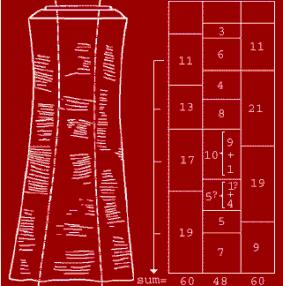
Nhìn sơ đồ trên, ta thấy cột bên trái gồm có 4 cặp số “11, 13, 17, và 19” đây là 4 cặp số nguyên tố (Prime number),

Thử hỏi Tiền nhân ta có biết gì số nguyên tố nầy không? Xin thưa rằng có, nhưng Tiền nhân ta không ghi số nguyên tố trên xương, trên đá, mà lấy số nguyên tố đặt tên cho sông núi cuả Quê hương Việt Nam chúng ta:  Nhị hà,  Tam đảo, Ngũ hoành sơn và cuối cùng là Thất sơn, ta có 4 số nguyên tố đầu tiên cuả dãy số là 2, 3, 5, 7 nếu dựa theo toán học suy diễn thì Tiền nhân ta và những người cỗ Phi châu có bà con, họ hàng với nhau, mà Tiền nhân ta là Anh nên lãnh 4 số đầu tiên 2, 3, 5, 7, còn Phi châu là Em nên lãnh 4 số kế tiếp 11, 13, 17, 19

Cảm ơn TS đã cho phép tôi trình bày một số vấn đề.

Kính

Võ Văn Rân