
Diophantine Equation mở rộng 4 ẩn số
Phần nầy tương đối khó, nhưng thời gian không cho phép ta kéo dài phần Phương trình Diophantus 3 ẩn số với 3 nhóm “a∙xn + b∙yn = c∙zn” cuả phần 8, nhiều lần nửa. Ta sang phần Phương trình Diophantus 4 ẩn số, với 4 nhóm (4 term) có dạng tổng quát sau
a∙vn + b∙xn + c∙yn = d∙zn
Giải phương trình Diophantus có 4 ẩn số và 4 nhóm như: {a∙vn }, {b∙xn }, {c∙yn }, {d∙zn}, ta phải đưa phương trình Diophantus nầy về 3 nhóm cùng dạng với phương trình Fermat’s Last Theorem “ x n + y n = z n ” có 3 nhóm {x n}, {y n} và {z n}.
Từ 3 nhóm nầy ta mới áp dụng được phương pháp tổng hợp, giửa Đông và Tây hay tổng hợp giửa Toán học Bình dân và Fermat’s Last Theorem sau đây
ζ(s) = an + bn = 1
b = n√(1 – an)
ζ(s) = 1 và ζ(1) ≠ 0
0 < α < 1, n –> ∞
x = (a∙z n√c) / ( n√a)
y = b∙z
= [n√(1 – an) ∙z n√c] / (n√b)
Lẻ ra phần lý thuyết phải được viết thật dài mới diễn tả đầy đủ cách xử dụng phương pháp tổng hợp, nhưng phần nầy xin dành lại cho quý vị có quan tâm đến toán học sau nầy, ở đây chúng ta chú trọng đến phần thực hành nhiều hơn, hy vọng các bạn trẻ sẽ thoải mái khi giải các phương trình Diophantus sau đây
Phần lý thuyết chỉ đơn giản vậy thôi
1*) Giải phương trình Diophantus sau:
a∙v8 + b∙x8 + c∙y8 = d∙z8
Tìm giá trị v, x, y, z nguyên
Cho biết z = 371 và gcd(v,x,y) = δ (δ > 1)
Giải
a· v8 + b· x8 + c· y8 = d· z8 (1)
Phương trình Diophantus (1) nầy có 4 ẩn số tương đương 4 nhóm so với Fermat’s Last Theorem có 3 nhóm
Theo đề ta có gcd(v,x,y) = δ (δ > 1)
suy ra
v ≡ modδ
x ≡ modδ
y ≡ modδ
Thật ra ta không cần phải cho biết trước gcd(v,x,y) = δ (δ > 1), vì Định lý sau cùng cuả Fermat đã được chứng minh, thì v,x,y, của phương trình Diophantus muốn có nghiệm nguyên, phải chia đúng cho một số lớn hơn 1, nhưng sợ có nhiều bạn trẻ khó tính nên phải cho biết trước.
Nói tóm lại các bạn trẻ gặp phương trình Diophantus không nói đến “gcd” (greatest commom divisor) hoặc “gcf” (greatest commom factor) hay “hcf” (highest commom factor), ta cứ hiểu, muốn phương trình Diophantus có nghiệm nguyên, thì các ẩn số phải chia đúng cho một số lớn hơn 1,
Trở lại vấn đề thay thế các giá trị tương đương x, và y để viết phương trình Diophantus từ 4 nhóm về dạng 3 nhóm như sau
{a· v8 }+ {b· x8 }+ {c· y8 } = {d· z8 }
{ a· v8 }+ {(b + c) · modδ8 } = {d· z8 } (2)
Viết lại phương trình (2) dưới dạng tổng quát Fermat Equation
xn + yn = zn
Đặt x = 8√a · v
y ≡ 8√(b + c) · modδ
z = 8√d · z
Phương Trình (2) viết lại
(8√a· v)8 + [8√(b+c)· modd]8 = (8√d· z)8 (3)
Muốn giải phương trình Diophantus (3), ta phải viết đầy đủ phương trình (3) có nghĩa là ta đi tìm giá trị các cơ số a, b, c, d của phương trình Diophantus(3)
Bài toán chưa cho biết a nên ta phải tìm bất cứ giá trị nào của a ( e.g. a = 4/7) thích hợp cho phương trình vì z = 371
Theo phương pháp tổng hợp ta có
ζ(s) = an + bn = 1
Suy ra β = 8√(1 – α8 ) = 8√{1 –(4/7)8}
β = 8√(5699265) / 7
Để dể tính ta chọn a = d = 1
ta chỉ cần tìm giá trị cuả b và c
Muốn tìm b, c ta dựa vào a và β = 8√(1 – a8)
a = 1
b = 5622777 = 38 x 857
c = 76488
d = 1
Thay các giá trị a, b, c, và d vừa tìm vào phương trình Diophantus
v8 + [8√(5622777 + 76488)· modd]8 = z8 (4)
Từ phương pháp tổng hợp :
ζ(s) = a8 + b8 = 1
b = 8√(1 – a8)
ζ(s) = 1 và ζ(1) ≠ 0
0 < α < 1
x = (a∙z 8√c)/( 8√a)
y = b∙z
= [8√(1 – a8) ∙z 8√c]/(8√b)
Ta có
x = (a∙z 8√c)/( 8√a)
Thay thế
x = 8√a · v
a = 1
suy ra
v = (a∙z 8√c)/( 8√a)
v = (4/7)∙371 = 212
v = 212
y ≡ 8√(b + c) · modδ
y = b∙z = [8√(1 – a8) ∙z 8√c]/(8√b)
8√(b + c) · modδ ≡ 8√(5622777 + 76488)· modd
hay modδ ≡ b∙z = [8√(1 – a8) ∙z 8√c]/(8√b) ≡ mod53
Ta có
b = 857
x ≡ modδ ≡ mod53 suy ra
x = 159
và
c = 76488
y ≡ modδ ≡ mod53
suy ra
y = 53
Thay các giá tri v, x, y, vào phương trình Diophantus (1) thử lại
a· v8 + b· x8 + c· y8 = d· z8
v8 + 857· x8 + 76488· y8 = z8
2128 + 857· 1598 + 76488· 538 = 3718 = 358914725543104304161
Các giá trị của v, x, y, thoả mản (1)
Đáp số:
a = 1
b = 857
c = 76488
d = 1
v = 212,
x = 159,
y = 53
z = 371
2*) Giải phương trình Diophantus có dạng sau:
a∙v11 + b∙x11 + c∙y11 = d∙36511
Tìm giá trị v, x, y, nguyên
Cho biết α = 0.6
Giải
Tương tự như trên
a∙v11 + b∙x11 + c∙y11 = d∙36511 (1)
Phương trình Diophantus (1) có 3 ẩn số v, x, y tương đương 4 nhóm:
{a∙v11}, {b∙x11},{c∙y11}, {d∙36511
Theo Phương pháp bình dân các giá trị cuả v, x, y phải có gcd(v,x,y) = δ (δ > 1)
Ta viết lại
v ≡ modδ
x ≡ modδ
y ≡ modδ
Thay thế các giá trị tương đương v, và x ta viết phương trình Diophantus từ 4 nhóm còn lại 3 nhóm như sau
a· v11 + b· x11 + c· y11 = d· z11
(a + b) · mod δ11 + c· y11 = d· z11 (2)
Viết lại phương trình (2) dưới dạng Fermat Equation
xn + yn = zn
Đặt x ≡ 11√(a + b) · modδ11
y = 11√ c· y11
z = 11√d · z
Phương Trình (2) viết lại
{ 11√ (a + b) · modδ}11 + (11√c· y)11 = (11√d· z)11 (3)
Chúng ta tìm giá trị các cơ số a, b, c, d của phương trình
Ta có
ζ(s) = a11 + b11 = 1
Suy ra β = 11√(1 – α11 ) = 11√{1 –(3/5)11}
β = 11√(48650978) / 5
Tìm giá trị các cơ số a, b, c, d cuả phương trình, hay nói cách khác là viết phương trình Diophantus sang dạng Fermat Equation
Để dể tính toán ta chọn giá trị c = 311, d = 211 ta chỉ cần tìm giá trị cuả a và b
Muốn tìm a, b ta cũng dựa vào giá trị cuả a và β = 11√(1 – a11)
a = 883426
b’ = 47767552 = 211 x 23324
c = 311
d = 211
Thay các giá trị vừa vào phương trình Diophantus ta có
{ 11√ (a + b) · modδ}11 + (11√c· y)11 = (11√d· z)11
{ 11√ (883426 + 47767552) · modδ}11 + (3· y)11 = (2· z)11 (4)
Áp dụng Phương pháp tổng hợp giải phương trình (4) ta có
ζ(s) = a11 + b11 = 1
b = 11√(1 – a11)
ζ(s) = 1 và ζ(1) ≠ 0
0 < α < 1
x = (a∙z 11√c)/( 11√a)
y = b∙z
= [11√(1 – a8) ∙z 11√c]/(11√b)
Ta có
x = (a∙z 11√c)/( 11√a)
Thay thế
x = 11√(a + b) · modδ11 ≡ 11√ (883426 + 47767552) · modδ
hay modδ ≡ (a∙z 11√c)/( 11√a) ≡ mod73
Ta có
a = 883426
v ≡ modδ ≡ mod73 Suy ra
v = 73
b’ = 47767552 = 211 x 23324
x ≡ modδ ≡ mod73 suy ra
x = 146
Giá trị thực tại cuả b = 23324
y = b∙z = [11√(1 – a8) ∙z 11√c]/(11√b)
y = 73
Thay các giá tri cuả cơ số, và các ẩn số mới tìm v, x, y, z vào phương trình Diophantus (1)
thử lại
a∙v11 + b∙x11 + c∙y11 = d∙36511 (1)
883426∙14611 + 23324∙29211 + 177147∙14611 = 2048∙36511
= 31372668556835970837700000000000
Các giá tri cuả cơ số, và các ẩn số mới tìm đúng là nghiệm ta muốn tìm
Đáp số:
a = 883426
b = 23324
c = 177147
d = 2048
v = 146,
x = 292,
y = 146
z = 365
Trong phần giải các phương trình Diophantus ở trên có đôi chổ hơi tối nghĩa, đó chính là nơi để các bạn trẻ them phần lý giải cuả mình sao cho hợp lý, còn đối với sinh viên nước ngoài tôi chỉ nói áp dưng phương pháp … và cho ra đáp số ngay, chứ không giải thích nhiều, tương tự như các nhà toán học họ chỉ đưa ra đáp số, chứ không giải thích làm cách nào để có đáp số
Các bạn thử áp dụng phương pháp tổng hợp giải các phương trình Diophantus sau
Bài tập
4*) Viết phương trình Diophantus sau:
a∙v2 + b∙x2 + c∙y2 = d∙z2
Tìm giá trị v, x, y nguyên
Cho biết z = 31
5*) Viết phương trình Diophantus sau:
a∙v3 + b∙x3 + c∙y3 = d∙z3
Tìm giá trị v, x, y, z nguyên
Cho biết α = 0.8
6*) Viết phương trình Diophantus sau:
a∙v4 + b∙x4 + c∙y4 = d∙z4
Tìm giá trị v, x, y, z nguyên
Cho biết α = 0.6
7*) Viết phương trình Diophantus sau:
a∙v6 + b∙x6 + c∙y6 = d∙z6
Tìm giá trị v, x, y, nguyên
Cho biết z = 351
8*) Viết phương trình Diophantus sau:
a∙v7 + b∙x7 + c∙y7 = d∙z7
Tìm giá trị v, x, y, z nguyên
Cho biết gcd(v,x,y) = δ (δ > 1)
9*) Viết phương trình Diophantus sau:
a∙v8 + b∙x8 + c∙y8 = z9
Tìm giá trị v, x, y, z nguyên
10*) Viết phương trình Diophantus sau:
a∙v9 + b∙x9 + c∙y9 = z10
Tìm giá trị v, x, y, z nguyên
TRANG GIẢI TRÍ MA TRẬN
Thời học trò, thầy cô giáo có chỉ sơ qua cách tìm ma trận 3 x 3 hay n = 3, rất thích thú nhưng chỉ biết có vậy thôi! còn với các ma trận lớn hơn n > 3 chưa bao giờ biết đến. Sau khi định cư tại Hoa kỳ có điều kiện, đọc nhiều liệu về toán, song chưa đầy đủ, xin trình bày để quý vị và các bạn trẻ cùng tìm hiểu, giải trí cho vui, dĩ nhiên có nhiều cách viết:
PHƯƠNG PHÁP tìm MA TRẬN LẺ
Tổng số ngang, dọc và chéo của ma trận lẻ như 3, 5, 7 …(2k+1) được viết theo phương pháp sau đây, có thể nói khi vẻ xong hình ma trận và phần phụ, ta cứ thế mà viết, không cần suy nghỉ, không cần tính toán
MA TRẬN (3 x 3) hay n = 3
Trước tiên ta vẻ 9 ô chính, xong ta vẻ 3 ô phụ ở trên và 3 ô phụ bên phải
số 1 được viết ô giữa trên cùng. Số 2 chéo lên phải nằm ở ô phụ, ta phải chuyển xuống ô chính, cùng hàng, dưới cùng. tiếp tục
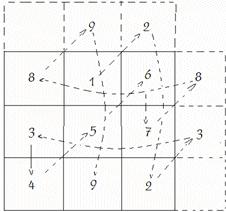
MA TRẬN (5 x 5) hay n = 5
Tương tự như trên khi đã vẻ xong hình, ta viết một mạch theo phương pháp, không cần tính toán gì cả
* viết số 1 ô giửa trên cùng, theo hướng chéo lên như H2
* số 2 viết ô phụ vẻ thêm, xong ta dời số 2 xuống ô cuối cùng (cùng hàng dọc)
* số 3 ở ô chéo trên, số 4 ô phụ bên phải, đưa số 4 sang bên trái(xem H2)
* số 6 nếu viết chéo lên đụng số 1, nên ta hạ xuống hàng dưới tiếp tục viết chéo lên phải …

Ví dụ ma trận bắt đầu từ 7, 8, 9, 10, ….. 31, ta viết số 7 ở ô giửa thay cho số 1 rồi tiếp tục như thường lệ (xem H3)
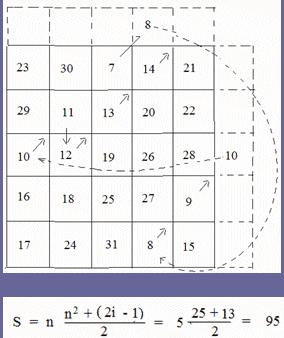
Chúc quý vị và các bạn giải trí vui vẻ
Ma trận (7 x 7), với 49 số, bắt đầu từ 3, 4, 5 …
Ma trận (9 x 9), với 81 số, bắt đầu từ 4, 5, 6 …
Ma trận (11 x 11) , (13 x 13), (15 x 15) ….
Võ Văn Rân
11 tháng 03 năm 2010
® nguồn “www.khoahoc.net”










































One Comment
wendy duong
Toi nhin vao thi khong hieu gi ca. ma cung khong doc no^?i. Tac gia co the nao cho thi du, ap dung quy luat nay vao doi song binh dan thuong ngay de cho toi hieu duoc khong?