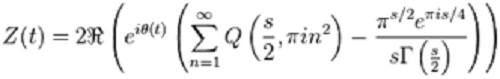Vo Văn Rân: RIEMANN HYPOTHESIS

MỞ ĐỀ

Kính thưa quý vị và các bạn trẻ

Để chào mừng THIÊN NIÊN KỶ THỨ III. Tháng 5 năm 2000, những ngày, tháng, năm cuối cùng của THIÊN NIÊN KỶ THỨ II, Hội Nghị Toán Học được tổ chức tại Collège de France, các nhà Toán học đã đúc kết 7 vấn đề tồn tại của hiên niên kỷ, có thể nói là hóc búa nhất, Clay Mathematics Institute viết tắc là CMI ứng ra 7 trịêu đô la, còn gọi là Millennium Prize Problems để thưởng cho bất cứ ai giải được các vấn đề trên, tương ứng mỗi vấn đề 1 triệu đô.

Thời gian đó tôi là công nhân, nên ít để ý đến các vấn đề bên ngoài công ty, nhưng tình cờ có một GS Đại học người Mỹ ở Fl, email cho tôi “7 problems”, lúc đó tôi không biết 7 problems là gì, phải vào Google tìm kiếm mới biết 7 problems là Millennium Prize Problems, sau khi đọc đi, đọc lại nhiều lần, tôi chọn 2 vấn đề dưới đây

The Birch and Swinnerton-Dyer Conjecture
The Riemann Hypothesis

Tại sao phài chọn 2 vấn đề, kính thưa quý vị tôi nghỉ rằng ngoài Việt nam, tôi còn quê hương thứ 2 là Hoa kỳ, do đó tôi phải chọn 2, nếu giải được 2 vấn đề của Thiên niên kỷ, thì đây là 2 món quà quý giá nhất dành cho Việt nam và Hoa kỳ.

DẨN CHỨNG

Chứng minh The Birch and Swinnerton-Dyer Conjecture hoàn tất và tôi đã gởi đến AMS tháng 4 năm 2001 như email trả lời dưới đây:

From : “Maria D’Arezzo” mld@ams.org

Sent : Tue, 17 Apr 2001 11:51:53 -0400 (EDT)

To: vo_ran@hotmail.com

Subject : “Proof of the Brich and Swinnerton-Dyer Conjecture”

Dear Dr Van Vo,

This will confirm receipt of your above paper, submitted to Proceedings of

the American Mathematical Society for consideration to publish.

The paper has been forwarded to the Proceedings Editorial Committee. You

will hear directly from the committee when a decision is reached.

Thank you for your interest in the American Mathematical Society

Maria D’Arezzo

Lần thứ 2 tôi gởi tới AMS Journal ngày 25/5/2004, AMS đã hồi báo như sau:

Dear Ran Van Vo,

We received your paper, “The Birch and Swinnerton-Dyer Conjecture”. Our policy is to suggest that you look at the AMS journals web site:

/and choose the journal that best suits your paper and follow the “peer-review submission” instructions on the specific journal website.

Good luck!

Thank you, Vickie Ancona Managing Editor, Book and Journal Production American Mathematical Society

Lần gởi thứ 2, cùng năm 2004 với nhà toán học Liên sô Grigori Y. Peralman, ông cũng giải được 1 trong 7 vấn đề là Poincare Conjecture, từ 2004 đến 2006, tôi và nhà toán học Liên sô không gặp sự phản bác nào.

KẾT QỦA

Đúng lý ra năm 2006 CMI phát thưởng Millennium Prize Problems cho tôi và nhà toán học Liên sô, nhưng sự việc không suông sẻ như vậy, ông chủ tịch (?) CMI bay sang Liên sô, mời Grigori Y. Peralman sang Madridthủ đô Tây Ban Nha nhận 1 triệu đô với giải thưởng Field Medial, nhưng ông đã từ chối.

Grigori Y. Perelman chứng minh the Poincare Conjecture, một trong 7 vấn đề của Millennium Prize, mà lại trúng thưởng Field Medial một giải thưởng nhỏ, cứ 4 năm một lần, giá trị tiền thưởng của Field Medial là $15.000 Canada, tương đương với 10.000 Euro ở thời điểm nầy, từ 2006 đến năm 2010, không thấy ai binh vực cho Grigori Yakovlevich Peralman, nên tháng 3 năm 2010 tôi đã viết bài ‘đúng hay không đúng’ để phân tích sự vô lý đó, xin trích một đoạn sau đây:

“Tôi xin trình bày một số vấn đề, khác biệt cuả các giải thưởng để quý vị và các bạn trẻ đánh giá xem “đúng hay không đúng”, để tôi khỏi bận tâm

Chúng ta, ai cũng nhận biết rằng 2 giải thưởng MILLENNIUM PRIZE PROBLEMS và FIELDS MEDALS hoàn toàn khác nhau,

khác về nguồn tiền dùng để phát thưởng, F. Medals có trước, dĩ nhiên họ có cơ quan quản trị tài chánh riêng, còn CMI có 7 triệu USD cho 7 vấn đề, do đó không thể lấy tiền CMI phát thưởng cho F. Medals, hay ngược lại
khác về mục tiêu để được xét phát thưởng. CMI đưa ra 7 vấn đề, ai giải được 1 trong 7 vấn đề, mới được nhận 1 trong $7 triệu, còn F. Medals không đặt vấn đề trước, chỉ yêu cầu có nhiều nghiên cứu đóng góp cho Toán học ….
khác về thời gian Fields Medals 4 năm 1 lần, Millennium Prize Problems không hạn định thời gian, chỉ khi nào có người chứng minh được, phải đăng trên báo khoa học có tầm vóc Quốc tế, để cộng đồng Toán học phân tích đúng sai trong vòng 2 năm, có cả ban cố vấn cuả CMI …
Millennium Prize Problems không thấy hạn định tuổi tác, Fields Medals không quá 40 tuổi
Fields Medals bắt đầu năm 1936 đến nay, không có thời gian chấm dứt, Millennium Prize Problems, bắt đầu từ năm 2000, sẽ chấm dứt khi 7 vấn đề được giải quyết xong…”

Tháng 3 năm 2010 sau bài phân tích của tôi, CMI mời nhà toán học Liên sô Grigori Y, Peralman đến nhận giải thưởng 1 triệu đô, đúng với tên của nó là Millennium Prize Problems. Hoan hô CMI đã làm đúng chức năng của mình, chứ không nhờ ai phát, nhưng ông vẫn từ chối

Tóm lại CMI loại tôi ra khỏi sân chơi, bởi Field Medidal, chỉ dành cho các nhà toán học trẻ dưới 40 tuổi, lúc nầy tôi đã ngoài 60 tuổi.

Kính thưa quý vị và các bạn trẻ, qua vấn đề The Birch and Swinnerton-Dyer Conjecture tuy không nhận được giải thưởng Millennium Prize Problems của CMI, nhưng tôi rất vui, và hảnh diện, vì sách của tôi đã được Cộng đồng Toán đón nhận, như một món quà dành cho các bạn trẻ Học sinh, Sinh viên, và các Độc giả có quan tâm về toán. Tôi vô cùng cảm ơn các nhà Toán học, các GS, LS và độc giả, chính nhờ quý vị đã giúp cho sách tôi được tồn tại đến nay.

NHÌN LẠI

Từ khi cộng sản Liên sô sụp đổ, Liên bang Sô viết tan rả, nhân tài cũng đã phân tán đến từng quốc gia tự trị, vậy mà Liên sô đã giải được 1 trong 7 vấn đề của Thiên niên kỷ.

Nhìn lại Hoa kỳ là nơi tập trung những Thiên tài Toán học của thế giới, mỗi ngày một đông hơn, vậy mà 15 năm qua kể từ năm 2000 đến 2015, chưa giải được vấn đề nào trong 7 vấn đề đó. Quý vị thấy có buồn không, riêng tôi cảm thấy buồn lắm, vì tôi cũng là công dân Hoa kỳ, suốt 15 năm qua chưa làm xong nhiệm vụ mà tôi hằng mong ước, khi đặt chân đến phần đất tự do nầy.

Hy vọng mộtngày đẹp trời, tôisẽ giải Riemann Hypothesis cùng với quý vị, chứ không thì các bạn trẻ lại bảo Ông già mắc dịch thấy đô la là mắt sáng rực, cũng đúng, thấy tiền không ham, chắc là bịnh rồi. Tôisẽ giải Riemann Hypothesis bằng ký hiệu R(o), (Rlà Rân, o là số lẻ hay ông già mắc dịch cũng được) như bao nhiêu ký hiệu khác của toán học,

Tỷ dụ

Trong ký hiệu nầy có R, nhưng R nầy là Riemann, mời quý vị đón xem, thấy mới tin

Con đường chúng ta đi còn xa vời vợi, mục tiêu không phải dừng lại ở những giải thưởng của MILLENNIUM PRIZE PROBLEMS hay FIELDS MEDALS, mà ta phải tiến xa hơn nửa, để giải quyết nhiều vấn đề tồn đọng trong quá khứ như DIOPHANTINE EQUATION chưa có phương pháp chung để giải, ‘… Indeed, in 1970 Yu. V. Matiyasevich showed that Hilbert’s tenth problem is unsolvable, i.e., there is no general method for determining when such equations have a solution in whole numbers.’ và nhiều vấn đề khác

ĐỌC TRƯỚC

Kính mời quý vị và các bạn trẻ đọc kỷ bài toán Riemann Hypothesis, và lên mạng internet xem hàng ngàn trang viết về Riemann Hypothesis của các nhà toán học trên Thế giới từ hàng 100 năm nay, có vậy mới so sánh được phần giải đáp của người VN mình đúng sai thế nào …

Phương pháp giải Riemann Hypothesis, tôi đã nhờ Luật sư copyright tại Thư viện Quốc hội Hoa kỳ trên mười năm, chứ không phải mới giải hôm nay, hay chưa giải. Khổ nổi lâu quá, tôi quên hơi nhiều, tôi nghỉ không lâu nửasẽ quên hết, lúc đó quý vị có đọc phương pháp ở Thư viện Quốc hội Hoa kỳ cũng khó giải được, ngoài ra tôi còn nhiều cách giải khác, chứ không phải chỉ có một cách giải duy nhất

RIEMANN HYPOTHESIS

Some numbers have the special property that they cannot be expressed as the product of two smaller numbers, e.g., 2, 3, 5, 7, etc. Such numbers are called prime numbers, and they play an important role, both in pure mathematics and its applications.

The distribution of such prime numbers among all natural numbers does not follow any regular pattern. However, the German mathematician G.F.B. Riemann (1826 – 1866) observed that the frequency of prime numbers is very closely related to the behavior of an elaborate function

ζ(s) = 1 + 1/2^s + 1/3^s + 1/4^s + …

called the Riemann Zeta function. The Riemann hypothesis asserts that all interesting solutions of the equation

ζ(s) = 0

lie on a certain vertical straight line.

This has been checked for the first 10,000,000,000 solutions. A proof that it is true for every interesting solution would shed light on many of the mysteries surrounding the distribution of prime numbers.

This problem is: Unsolved

NGUỒN GỐC RIEMANN HYPOTHESIS

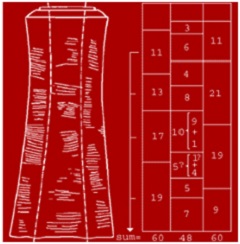Bài toán Riemann Hypothesis có nguồn gốc từ gần 40.000 năm trước

Các nhà khảo cổ mới đây đã tìm thấy khúc xương hóa đá gần bốn chục ngàn năm trước (40.000 – 30.000) ở Phi châu, hay vùng Trung á, tôi có đọc nhưng quên. Trên khúc xương hóa đá có ghi khắc những con số như minh họa.

Nhìn sơ đồ minh họa, khúc xương hóa đá, ta thấy có ba hàng số chạy dọc theo khúc xương, hàng bên trái, hàng giữa và hàng bên phải mà các thợ săn, hay các nhà làm lịch, ghi khắc lên xương.

Hàng bên trái có 4 cặp số 11, 13, 17, 19 là 4 số nguyên tố, chúng ta vô cùng kinh ngạc, cách nay gần bốn chục ngàn năm (40.000) mà con người đã biết đến các con số nguyên tố,

Bài toán về phân phối số nguyên tố hay Riemann Hypothesis đến nay vẫn còn bỏ ngỏ

Thử hõi Ông bà chúng ta xưa kia có biết gì về số nguyên tố không ? Xin thưa rằng, biết, mà còn biết rành hơn chúng ta, tỷ dụ dùng 4 con số nguyên tố đầu tiên là 2, 3, 5, 7 đặt tên cho sông núi VN: Nhị hà, Phá Tam giang, Ngủ hoành sơn và Thất sơn, 4 số tiếp theo là 11, 13, 17, 19 cộng chung là 60, ông bà xưa kia dùng làm lịch vạn niên cứ 60 năm giáp lại một vòng, tỷ dụ tuổi Giáp ngọ thì 60 năm sau trở lại Giáp ngọ. Khi Ông bà ta đã biết xử dụng tiền trả lương hay mua bán, thì con số 60 cũng được dùng trong đơn vị tiền tệ, như 1 quan là 600 tiền, 1 tiền là 60 đồng, qua các số nguyên tố chúng ta thấy Ông bà xưa kia có liên hệ ít nhiều đến nhóm người có xương hóa đá.

TÓM LẠI

Tôi đưa ra những dẩn chứng ở trên, để chứng tỏ tôi nói có sách mách có chứng, mong quý vị thông cảm cho, chứ không trách cứ ai cả, làm toán đã nhức đầu rồi, mà giận người nầy hay trách người kia, thì còn sức đâu mà làm toán. Các bạn trẻ muốn giỏi toán không khó, trước hết phải loại bỏ những ý nghỉ không tốt, trong đầu óc mình ra, nhất là không dùng những chất kích thích, rượu bia thuốc lá, xì ke, v.v. tiếp theo là bồi dưỡng trí tuệ, bằng vui chơi lành mạnh, giúp đở gia đình, bạn bè và xã hội, thường xuyên tập thể dục, dĩ nhiên còn nhiều phương pháp. Khi tinh thần ổn định, trí óc minh mẩn, lúc đó các bạn muốn làm việc gì, thì tập trung tất cả vào việc đó, chắc chắn các bạn sẽ thành công. Tiếc quá hồi nhỏ tôi không lo học, Đến nay tôi hiểu thì tôi đã muộn rồi, tuổi gìa đã đến, không thể từ chối, nhưng còn nước còn tác phải không quý vị

Trước thèm năm mới 2015, và Tết cõ truyền sắp đến kính chúc quý vị, quý quyến và các bạn trẻ năm mới sức khỏe an vui, mọi sự như ý.

Võ Văn Rân

Vo Văn Rân: RIEMANN HYPOTHESIS

About the author

Related Articles

Leave a Reply